Human memory has holographic properties, which can be pretty weird. When you cut an ordinary photograph into quadrants, you get four separate pieces of the photo. When you cut a hologram into quadrants, each piece contains the entire image, just smaller and with less resolution.
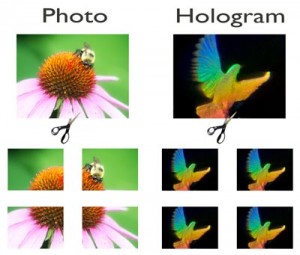
Cutting a hologram is weird.
That’s because the hologram is an interference pattern that is spread out over the whole image. To create one, you aim a laser beam at a half-silvered mirror, which splits it into two beams. You aim one of the beams at the object and aim the other beam at the film. The light that reflects off the object hits the film along with the other beam where they interfere with each other and leave a repeating pattern across the film. Each small spot contains a copy of the entire image, albeit at a low resolution. So you can chop it finer and finer and still see the whole image in each tiny hologram.
Similarly, our memories are spread out over our cerebellar cortex and damage to parts of it doesn’t remove specific features from memory. Studies by Karl Lashley in the 1950s showed that taking out patches of a rat’s cortex from different areas had no effect on the rat’s ability to remember a maze. Wherever the rat was storing its memory of the maze, it didn’t seem to be concentrated in any one area. Rather, the information seemed to be spread over the whole cortex. In the brain, redundancy seems built-in.
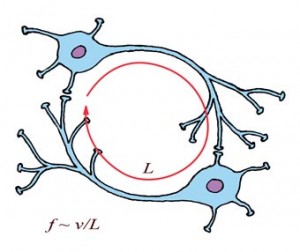
So, it seems, memory shares some of the strange features of a hologram, but that doesn’t prove that memory is actually a hologram. There may be other ways to distribute information, and resonant memory is one of them: recruiting neural loops with resonance could easily involve the actions of dozens or hundreds of loops with the requisite frequency.
However, it is intriguing that holographic interference patterns can be computed with Fourier transforms, providing a close mathematical link to ideas of resonant memory. They may in fact have hidden correlations, even if the mechanics end up being different.
Several researchers were puzzled and excited by Lashley’s results. In the 1960s, the neurosurgeon and psychiatrist Karl Pribram was influenced by physicist David Bohm to apply principles of holography to the brain as a computing mechanism. The theory is enticing, but the details remain a little fuzzy. Pribram called his theory holonomics, and it is one of the inspirations for the theory of resonant memory. On some level, both theories may be manifestations of the same underlying mechanism.
Pribram’s theories have been co-opted by new-age spiritualists, who think it may bridge the gap between science and spiritualism. This may have led many serious researchers to discount holonomics. However, the same new-agers have found ways to wring spiritualism out of quantum mechanics as well, and that hasn’t affected its utility in physics. Ultimately, holonomics must be judged by its accuracy, not its acolytes.
We’re not quite done with the strangeness of holography. As we just discussed, when you expose a normal hologram, you interfere the light of a plain laser with light that has scattered off your object. However, there is a holographic trick: instead of using a plain laser, you can use a second object to produce interference. In that case, if you make a hologram of an apple interfering with an orange, you will subsequently see the apple when you look through the hologram at an orange, and vice versa. Thus, you have a level of interconnected data built into the system. Correlating separate memories like this is just built in to the mathematics of holography.
This might mean that the roar of a lion gets cross-referenced with a desire to climb a tree. By linking two ideas together like this, you might guarantee an immediate response that could save your life. Unfortunately his is not a built-in feature of resonant memory theory. Instead, the same kind of cross wiring probably comes from growing nerve cells in the hippocampus that physically stitch memories together. We’ll return to this problem later.
References
Lashley, K. In Search of the Engram in Psychological Mechanisms in Animal Behaviour. Academic Press, New York, 1950.
Pribram, Karl H. “Holonomy and Structure in the Organization of Perception.” Images, Perception, and Knowledge. Springer Netherlands, 1977. 155-185.