Tag Archives: frequency

How Might Resonant Memory Work?

Leave a reply

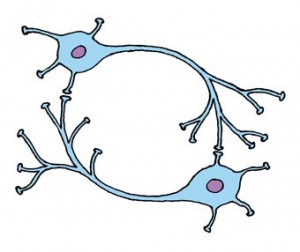
So how might resonant memory work? Here’s a highly simplified diagram:

two-neurons-plain

There are two neurons here, creating a loop. How likely is this to happen with millions of nerve cells spreading dendrites all over the cortex?

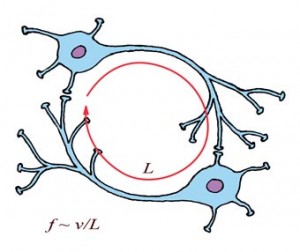
To the extent that it does happen, it could set up a loop with a specific frequency:

two-neurons-frequency

The frequency (f) of this loop is approximately equal to the nerve impulse velocity (v) divided by the length of the loop (L). This doesn’t take into account the time added by each synapse, but it’s a rough start. Whatever the velocities of each axon and the lag of each synapse, this particular little loop has a cycle time associated with it. If you hit it with an input with a matching cycle time, this loop will resonate:

two-neurons-spikes

The input stream has pulses separated by t, the cycle time of the loop. The first pulse to hit will circle the loop and feed back into the starting neuron, just as the second pulse is coming in. Because the body of the neuron sums the inputs, it will keep sending a strong signal through the loop. The synapses are strengthened when a signal continues to impact them, so this circuit starts to provide stronger and stronger resonant signals as time goes on. We are training this loop to respond to the input.

The output is just the same as the input here, so we haven’t really accomplished much. But we have seen just how easy it is to create a hypothetical neural circuit that can resonate with a given input.

 

Can Neurons have Resonance?

Leave a reply

It’s fun and easy to make a tuning fork resonate, but can we do the same thing with neurons?

There are a couple of tantalizing hints that we can. The inner ear is lined with tiny cilia that are each tuned to a specific frequency. When you hear a simple sine wave, only those cilia that are of the proper length will resonate. That signal is then transmitted to the brain and you can recognize the pitch. If you have perfect pitch, you might even be able to tell me the frequency of the tone.

Frog ear cilia

Fine as frog’s hair: inner ear cilia from a frog.

Most sounds are not single frequencies, though, and when the sound of a trumpet hits your ear, dozens of cilia will resonate, each one picking up a specific component of the sound. Based on the attack, sustain and decay of each of these components, a trained brain will determine that a trumpet made the sound.

When the inner ear does this, it performs what is called a Fourier decomposition of the sound. Fourier was a French scientist and mathematician in the 1700s who discovered that signals could be decomposed into a series of sine waves of varying frequency and amplitude. The richness of a trumpet blast is due to the unique set of frequencies that are produced, based on the shape of the trumpet.

Modern computers perform Fourier analysis all the time, but it is a time-consuming procedure. The magic of the inner ear is that the computation is done immediately, simply via resonance. No calculations required.

However enticing, hair cells in the ear are not neurons. Is there anything comparable in the brain? The answer is a resounding yes. Individual nerve cells can oscillate with different frequencies, as can groups of cells. Large ensembles of neurons can give rise to brain-scale oscillations like alpha waves, among others. The brain is simply buzzing with oscillations. Not unlike a room full of tuning forks.